Superelevation is the transverse slope along the width of the road provided by rising the outer edge of the road with respect to the inner edge, throughout the length of the horizontal curve. It is provided to facilitate the safe passage of the vehicle in a horizontal curve. The concept and formula for superelevation are discussed further.
Why Superelevation is Needed!
At every horizontal section of a road, the radius of the horizontal curve (R) becomes low as a result of which centrifugal force increases and acts outwards (i.e., away from the center) in the horizontal direction on the outer wheel.
The upper image represents the same with,
l - length of the vehicle,
b - the breadth of the vehicle,
R - radius of the horizontal curve,
P - the centrifugal force which is given by
P = (mv^2)/R
where,
m - the mass of the vehicle
v - velocity of the vehicle
Due to high speed and low radius at the horizontal curve, large centrifugal force develops which could lead to "overturning of the vehicle" or "skidding of the vehicle".
Overturning of the vehicle
The moment caused by centrifugal force about the outer wheel, Overturning moment (Mo),
Mo = P * h, h - height of C.G.
The moment caused by self-weight of the vehicle, Restoring moment (Mr),
Mr = (W * b)/2
For safe condition, i.e., no overturning, Mr > Mo, by which we get,
(W * b)/2 > P * h
b/2h > P / W
By substituting value for P = (mv^2)/R and W = mg, we get,
b/2h > (v^2)/(gR)
In this condition, no overturning occurs.
Skidding of the vehicle
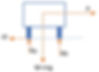
Ff - lateral frictional resistance, which is given by,
Ff = f * (Ra + Rb), where,
f - coefficient of lateral friction,
Ra + Rb = W (i.e., mg)
Ff = f * mg
For safe condition, i.e., no skidding, Ff > P, by which we get,
Ff > P
f * mg > (mv^2)/R
f > (v^2)/(gR)
In this condition, no lateral skidding occurs.
To have the above-mentioned safe conditions of no overturning and no skidding, the vehicular dimensions must be appropriate and the coefficient of lateral friction must also have an appropriate higher value. Unfortunately, both of which are not in control of a highway designer. Therefore, to have a safe passage through a horizontal curve superelevation is being introduced.
Superelevation Derivation
As said earlier, superelevation is the transverse slope along the width of the road, provided to develop centripetal force to counteract the centrifugal force. It is achieved by raising the outer edge with respect to the inner edge in a transverse direction for the total length of the curved section. The below figure could be referred for derivation.
For equilibrium condition in the transverse direction,
W*sinθ - P*cosθ + Ff1 + Ff2 = 0
P*cosθ - W*sinθ = R1 + R2
P*cosθ - W*sinθ = fN1 + fN2
P*cosθ - W*sinθ = f*(N1+N2)
P*cosθ - W*sinθ = f*(P*sinθ + W*cosθ)
P*cosθ - f*P*sinθ = W*sinθ + f*W*cosθ
P/W = (sinθ + f*cosθ)/(cosθ - f*sinθ), dividing by cosθ on R.H.S.,
(v^2)/gR = (tanθ + f)/(1 - f*tanθ)
Substituting tanθ = e,
v^2/(gR) = (e + f)/(1 - e*f)
As per I.R.C., f=0.15 and e is limited to 0.07 (for plain and rolling zone). Therefore e*f becomes 1.
v^2/(gR) = e + f
Superelevation Formula
e = rate of superelevation
f = design value of coefficient of lateral friction = 0.15
v = design speed of the vehicle, m/sec
R = radius of the horizontal curve, m
g = acceleration due to gravity = 9.8 m/sec^2
Substituting g = 9.8 and converting v to kmph, we get,
v = design speed of the vehicle, kmph
R = radius of the horizontal curve, m
With these formulas, e value could be found out. If f is taken as 0 (zero), then equilibrium superelevation could be found out. Suitable radius (R) for the constrained values of e and f could also be found out.
Limiting Superelevation
IRC provides limiting superelevation value for different zones, as follows,
Max Superelevation | Zone |
e ≤ 0.07 | Plain and rolling |
e ≤ 0.07 | Snowfall |
e ≤ 0.1 | Mountainous |
e ≤ 0.04 | Urban |
If in case for plain zone both e and f exceeds 0.07 and 0.15 respectively, then design speed(v) must be reduced or radius of the horizontal curve(R) must be increased.
Superelevation in Mixed Traffic Flow Condition
Vehicles do not have the same speed on a horizontal curve, therefore in such a case, only mixed traffic flow condition is present. For superelevation calculation in mixed traffic flow conditions, the speed shall be taken as 75% of design speed i.e., 0.75v, and the lateral friction 'f' shall be neglected for safe conditions. Superelevation formula now becomes,
e = (0.75 * v^2)/(127 * R)
e = (v^2)/(225 * R)
where,
v - design speed in kmph,
R - radius of the horizontal curve in m,
Practice Problem
For further clarifications and insights do check out the video lecture on horizontal curve design attached below.
Want to stay updated with the latest technical content and job notification blogs? Subscribe to our APSEd blog by providing your mail id below.